RPGツクールはシンプルな使い勝手にもかかわらず、 使い方次第で多彩なゲーム表現を可能とするツールです。 今回はそんなRPGツクールにて、隠されたアイテムを発見するダウジング機能を実装してみたいと思います。
そう、コモンイベントのみで……。

サンプル(RPGアツマール):
https://game.nicovideo.jp/atsumaru/games/gm11759
ココナラでRPGツクールMVのプラグイン製作サービスを出品してみたのですが、 依頼が来ないので宣伝というかパフォーマンスとしてやってみました。 コモンイベントは簡易版プログラムみたいなものなので、 プログラマならこんなこともできんだよ~ってことで。
はじめに
今回つくるダウジング機能はこんな感じの仕様です。
- プレイヤーがアイテムから一定距離内に近づくと反応する。
- 反応するとアイテムの存在する方向を指し示す。
- 指示点は常にゆっくりと揺れている。
- アイテムに近づくほど揺れが激しくなる。
一見するとプラグインの領域っぽい、というか、実際プラグインでやるべきものをあえて選んでみました。 この記事ではこれをコモンイベントで実現する方法を解説しますが、絶対に真似しないでください(!?)。 何故ならば、これは単なるパフォーマンスであって、とんでもなく効率の悪い方法だからです。
もし同じような機能が欲しい場合にはプラグイン製作者に頼んでみてください。 前述の通り、私は有料で製作サービスをやっていますし、 ツクール界隈には無料でプラグインを製作してくれる親切な人がたくさんいますので。
仕組みについてはプログラマ以外にも配慮して解説はしますが、プログラミング未経験者には結構難しいと思います。 どれくらい難しいかというと、プログラミング言語を覚えてプラグインとして同じものをつくる方が簡単かもしれないくらい難しいです。 逆に、この記事をすべて理解できたならプラグイン開発を始めてみるといいかもしれません。
と、まあそんなわけで、仕組み自体にそんなに興味のない人はさらっと眺めて、 プログラミングってこんなこと考えるんだなぁくらいに思ってもらえればこの記事は大成功です。 「コモンイベントの ちからって すげー!」っと言って帰りましょう。
実装方針
基本的な流れとして並列処理のコモンイベントで毎フレーム特定の処理をすることでダウジング機能を実装します。 フレームというのはゲームの更新処理一回分のことで、だいたい1秒間に60回程度実行されることが多いです (1秒間に実行されるフレーム数をFPSといいます)。 ゲームが動いているように見えるのは1/60秒ごとにこの更新処理によって絵が変化するためです。
毎フレーム実行する処理の概要は次の通りです。
- プレイヤー近辺のタイルにアイテムがあるか調べる。
- 一番近くにあるアイテムの方向に指示点を動かす。
- 適当に揺らしながら指示点を表示する。
具体的な処理内容は実際のコモンイベントを見ながら説明していきますが、 その前に次の内容について説明しておきます。
- コモンイベントと関数
- 位置の移動
- 三角関数
コモンイベントと関数
プログラミングでは「関数」と呼ばれる単位に処理を分割して整理するのが一般的となっています。 この名称はもちろん数学の関数から来ているのですが、表すものは少しだけ違います。 関数とは、いくつかの設定(入力)を受け取り、設定に従って処理をして、結果(出力)を返す、という流れに従った一連の処理を指します。 入力と出力はない場合もあります。
これだけ聞いてもいまいちピンとこないかもしれませんが、RPGツクールのイベントコマンドはだいたいこの関数の形になっています。 例えば、「指定位置の情報取得」コマンドについて考えてみましょう。 このコマンドでは、どの位置のタイルのどんな情報を取得したいかという『設定を受け取って』、 それに従った情報を取得する『処理をして』、指定された変数にその値を入れることで『結果を返します』。 他にも「所持金の増減」コマンドでは、 所持金をどれくらい増やすまたは減らすのかという『設定を受け取って』、 所持金を増減させる『処理をします』。 出力はありません。 「ゲームオーバー」コマンドでは、ゲームオーバーにする『処理をします』。 入力も出力もありません。 なんとなく関数のイメージが掴めたでしょうか?
さて、何故こんな関数の話をしたかというと、 コモンイベント自体もこの関数の考えに従って整理することができるからです。 今回実装したダウジング機能は30ものコモンイベントによって構成されていますが、 そのすべてが一画面に収まる長さの短いコモンイベントになっています。 実は長いコモンイベントにすれば2つに収まるのですが、 長いコモンイベントではどの部分で何をやっているのか把握するのが困難で理解しづらいのです。
一般にプログラマというと、特殊技能に精通した人というイメージが強いかもしれませんが、 実は「いかに文章(プログラム)をきれいにわかりやすく書くか」ということを真面目に考えている人たちだったりします。 正直、化学者や生物学者なんかよりは論説とかの物書きの方が近いんじゃないかと思ったり……。
閑話休題。
では、コモンイベントで関数をどう表現するかについて考えてみましょう。 関数は入力・処理・出力の三要素から成るのでした。 このうち処理はイベントコマンドを羅列するだけなので特別な機構は要りません。 入力や出力には「指定位置の情報取得」でも使っていたように変数を使います。 ただし、どの変数を使うかは決め打ちです。 「このコモンイベントの実行前には必ずこの変数とこの変数に値を設定してね」 「このコモンイベントの実行後はこの変数に結果が入ってるよ」 とあらかじめ決めておくことでコモンイベントの入力と出力を表現します。
関数には必ずその実行を指示する(「呼び出す」と言う)別の関数(コモンイベント)が存在します。 呼び出し側のコモンイベントでは、まず関数の仕様に従って必要な設定を変数に入れ、 「コモンイベント」コマンドを実行してから、関数の仕様に従って変数から値を取り出します。
これでコモンイベントで関数を表すことができました。 ……とはいっても、言葉の説明だけではなかなか理解しづらいかもしれません。 実際のコモンイベントの実装をみてみると理解しやすいと思うので、意識しながら読んでみてください。 特に「揺れの更新」あたりの実装は説明したことがそのまま反映されているのでわかりやすいと思います。
位置の移動
今回のダウジング機能の仕様には、指示点の表示位置を決めるための座標がいくつかあります。
- 表示の中心座標
- 指示点の目標位置
- 指示点の現在位置
- 揺れによる変位
これらを使ってどのように指示点の位置を計算するかについて説明します。
「表示の中心座標」は、指示点を含めたダウジング表示全体の中心となる座標です。 この値は設定として与えられる固定値であり、唯一の絶対座標です。 他の座標はすべて、この座標からの相対座標か、あるいはさらにそれの相対座標です。
「指示点の目標位置」と「指示点の現在位置」は、ダウジング表示上のどのあたりに指示点を表示するかです。 これらはともに中心座標からの相対座標になります。 目標位置はプレイヤーからアイテムに向かう方角上かつ円周上の点で、 指示点の現在位置は毎フレームこの点に向かって、設定された最大速度を超えないように移動します。
「揺れによる変位」はX方向とY方向それぞれの振動の合成による指示点の位置ずれです。 これは指示点の移動とは独立した運動であるため、指示点の現在位置からの相対座標になります。
まとめると次のようになります(min(a, b)はaとbの小さい方を表します)。
表示位置 = 中心座標 + 現フレームの現在位置 + 揺れによる変位
現フレームの現在位置 = 前フレームの現在位置
+ min(現フレームの目標位置 - 前フレームの現在位置, 最大移動速度)
三角関数
三角関数は今回の実装における最大の難所です。
方角から円周上の点を求めたり振動させたりと、 三角関数を使いたくなる仕様でいっぱいなのですが(もちろんわざとです)、 残念ながら……非常に残念ながらコモンイベントには三角関数を計算する機能はありません。 というか、まず小数がありません。
そこで、「小数をどう表現しようか」「三角関数をどうやって計算しようか」というのが、 この記事のプログラマ的見せ場となっております。 順に説明していきます。
小数の表現
コモンイベントでは小数を扱うことができません。
除算結果の小数点以下は切り捨てられるため、例えば1 / 2は0になります。
sinやcosが仮に計算できたとしても、そのままでは至る所で0になってしまいます。
円周率だって3です。
このままでは「ゆとり」だと揶揄されてしまいます。
小数を表現するアイデアというのは実は非常に単純で、単にn倍するだけです。
例えば、n=1000としましょう。
そのままでは1 / 2 + 1 / 2の結果は0ですが、
1000倍された状態で計算すれば、1000 / 2 + 1000 / 2で1000となり、
1000で割って戻してやれば1となって正しい計算結果になります。
さて、これはアイデアとしては単純ですが、実装するとなると結構ややこしかったりします。 先の例では分子だけを1000倍しましたが何故でしょうか? 掛け算の場合はどうすればいいのでしょう? 1000倍した数同士を掛けて、1000で割れば正しい結果になるでしょうか? ……n倍した数同士の演算手順については慎重に考える必要がありそうです。
まず、単純な四則演算について考えてみましょう。 計算に使う値と計算結果がそれぞれn倍された状態になるように注意すると、 四則演算は次のようになります。
n(x + y) = nx + ny n(x - y) = nx - ny n(x * y) = (nx * ny) / n n(x / y) = (nx / ny) * n = (nx * n) / ny
【xとyの演算結果のn倍】を、【xのn倍】と【yのn倍】と【n】による演算で表現できました。 割り算で計算順序を入れ替えていることに注意してください。 割り算をするとその時点で小数点以下が切り捨てられてしまうため、 先にn倍してから割った方が誤差が少なくなります。
次に複数の四則演算を組み合わせた演算についてですが、
可能な限り割り算の回数を少なくかつ後回しにすると計算誤差が減ります。
例えば、1 / 3 * 3を先ほどの四則演算の手順に従って計算してみましょう。
すべての数を1000倍して同等の演算に置き換えると次のようになります。
[ n(x / y) = (nx * n) / ny ] 1000 * (1 / 3) = (1000 * 1000) / 3000 = 333 [ n(x * y) = (nx * ny) / n ] 1000 * ((1 / 3) * 3) = ((1000 * (1 / 3)) * 3000) / 1000 = (333 * 3000) / 1000 = 999 1 / 3 * 3 = 999 / 1000 = 0
計算誤差のせいで正しい結果にはなりませんでした。
しかし、これを(1 * 3) / 3と変形してやれば当たり前ですが、正しい計算結果になります。
1 / 3 + 2 / 3なんかも同じで、(1 + 2) / 3としてやれば正しく計算できるようになります。
後述する三角関数の実装ではこのようなことに注意して計算しているため、 一見おかしな計算方法に見えるかもしれません。 しかし、計算誤差を抑えるためには必要な手順なのです。
これまでの説明と後述の三角関数の実装で一点だけ違うところとして、
説明では入力と出力のどちらもn倍された状態を考えましたが、
実装では入力をn倍、出力をm倍と値を変えています。
つまり、f(x * n) * mを計算するように三角関数は実装されています。
三角関数の計算
さて、小数の計算はできるようになりましたが、依然としてできるのは四則演算だけです。 なんとかして四則演算によって三角関数を計算しなければなりません。 そこで、マクローリン展開というものを使います。
マクローリン展開は関数f(x)と等価な多項式を求める方法です。 つまり、関数f(x)に対して次の式の定数anをすべて求めます。
微分やら階乗やら無限級数やらで複雑なので、マクローリン展開の詳しい説明はここではしません。 他所の解説を参照してください。 ここで重要なのは三角関数を多項式で表すことができるという点のみです。
とはいえ、変形結果は無限多項式なのでこれをそのまま計算することはできません。 ではどうするのかというと、最初の方のいくつかの項までだけ計算して残りは無視してしまいます。 「そんなことしていいの?」と思うかもしれません。 もちろん普通はダメです。 しかし、特定の条件下であればこれは近似式として使うことができます。 それはxの値が0に近いときです。
0に近い値、例えばx=0.1としましょう。 このときx2=0.01で、x3=0.001です。 後ろの方の項ほど非常に小さい値になるのがわかると思います。 非常に小さい値を足したり引いたりしたところで値が大きく変化することはないため、 これらは誤差として許容すれば無視することができます。
0に近い値というのがどれくらいまでなのかは許容できる誤差の大きさによりますが、 今回は絶対値が1以下の範囲くらいまでとして使っています。 これはそれなりに誤差が大きく、角度に数度のずれが生じますが、 指示点を揺らしたりしてごまかしているのでまず気づかれません。
今回の実装に必要な(逆)三角関数はarctan、sin、cosの三つです。
arctanはtanの逆関数で、tanθの値からθを求めます。
これらをマクローリン展開して、x3の項までとった結果は次の通りです。
ここでarctanについて、これは値域が-πからπであるためすべての角度を取得することができません。
しかし、今回はこれをアイテムのある方角の計算に使いたいのでそれでは困ります。
そこで、代わりにプログラミング言語でよく使われるatan2という関数を採用します。
これはxとyの二つの値を受け取って、(デカルト)座標(x,y)を極座標に変換した際の偏角を求めるものです。
xが正の値のとき、atan2(y,x)はarctan(y/x)に一致するため、実装にはarctanを使います。
前述したようにマクローリン展開による近似関数の有効定義域はせいぜい[-1, 1]です。 このままでは利用できないため、次の性質を利用して定義域を広めます。
atan2について。
まず、最初の式で第二象限と第三象限の計算を、第一象限と第四象限の計算に変換します。
そのあと、次の式で第四象限の計算を、第一象限の計算に変換します。
そして、最後の式でy > xの領域の計算を、y <= xの領域の計算に変換します。
これでy / xの取り得る値の範囲は[0,1]となり、マクローリン展開したarctanに適用できます。
sinとcosについて。
まず、最初の式で-πから0までの角度の計算を、0からπまでの角度の計算に変換します。
そのあと、次の式でπ/2からπまでの角度の計算を、0からπ/2までの角度の計算に変換します。
そして、最後の式でπ/4からπ/2までの角度の計算を、0からπ/4までの角度の計算に変換します。
これでマクローリン展開したsinとcosに適用できます。
なんとか三角関数を実装する目処が立ちました。
コモンイベント解説
各コモンイベントの解説です。
全部で30あるので、真面目に読むと死ねます。ほどほどに。
ダウジング機能

ダウジング機能の準備と後片付けです。 「ダウジング機能」スイッチが有効な間、動き続けます。
やっていることはダウジング機能に使う設定値や状態の初期化とピクチャのON/OFFです。 「ダウジング中」スイッチにより、ダウジング状態はON/OFFできるようになっているため、 それに合わせてダウジング表示に使うピクチャの表示・非表示を切り替えています。
設定の初期化

設定値の初期化です。
内容は次の通り。
| 設定 | 説明 |
|---|---|
| 最大有効距離 | アイテムが発見可能なマンハッタン距離 |
| 表示の中心座標 | ダウジング表示の中心座標 |
| 表示の半径 | 揺れを含まない指示点の移動円の半径 |
| 数値の精度 | 小数の計算のために数値に掛けられる倍率 |
| 最大移動速度 | 1フレームに移動できる最大の距離 |
| 揺れの振幅 | 揺れる幅の大きさ |
| 揺れの最小周期 | 最もアイテムに近づいたときの揺れ一周にかかる時間 |
| 揺れの最大周期 | 最もアイテムから離れたときの揺れ一周にかかる時間 |
| 揺れの初期位相 | 揺れが始まる角度 |
マンハッタン距離というのは、X方向とY方向の位置差分の絶対値を足し合わせたものです。 要はグリッド上を上下左右移動のみで移動した場合に最短ルートで何歩かかるか、 という測り方の距離です。
状態の初期化

フレーム間にわたって保持する必要のある状態の初期化です。
内容は次の通り。
| 状態 | 説明 |
|---|---|
| 現在位置の座標 | 現在の揺れを含まない指示点の座標 |
| 揺れの位相 | 現在の揺れの角度 |
ピクチャの表示

ダウジング表示のためのピクチャの表示です。
ピクチャの消去

ダウジング表示のためのピクチャの消去です。
ダウジング中

ダウジング中に毎フレーム実行される処理です。 「ダウジング中」スイッチが有効な間、動き続けます。
処理内容は次の通りです。
- プレイヤー近辺のタイルを調べてアイテムを探す。
- 最も近いアイテムの方角を示す指示点の目標位置を算出する。
- 現在位置から目標位置に向かって最大速度を超えないように移動する。
- 現在の揺れの状態を計算する。
- 現在位置に揺れを加えてダウジング表示を更新する。
タイル走査前の初期化

タイル走査中に参照あるいは操作する変数の初期化です。
「走査」というのはプログラミング用語で、 たくさんあるものをひとつひとつ調べることを言います。 英語のスキャン(scan)に対応する言葉だというとわかりやすいでしょうか(むしろわかりにくい?)。
タイル走査の目的は最も近くにあるアイテムをみつけることです。 そのためにはそれまでに発見した最も近いアイテムまでの距離を記憶しておき、 その距離と新しく発見したアイテムまでの距離を比較します。 新しいアイテムまでの距離の方が短ければ、それをその時点での最有力候補として記憶しておきます。 すべてのタイルを調べ終えた時点での最有力候補が最も近いアイテムです。
ただし、この方法には考慮すべき事項が二つあります。 ひとつは一番最初に発見したアイテムをどう扱うか、 もうひとつはアイテムをひとつも発見できなかった場合にどうするか、です。
前者について、最初のアイテムはもちろんその時点での最有力候補にすればいいのですが、 問題はそれが最初のアイテムであるとどうやって判断するかです。 適当な変数にそれまでの発見数を記憶しておいてもいいのですが、 ここでは「それまでに発見した最も近いアイテムまでの距離」を大きな値で初期化することで解決します。 なぜなら、この値が十分に大きければ最初のアイテムまでの距離は必ずそれより短いため、 特別扱いしなくても最有力候補になるからです。
また、この方法によって自動的に後者の問題も解決します。 もし、すべて調べ終えても「それまでに発見した最も近いアイテムまでの距離」が有効距離内にないのなら、 それは発見できなかったことに他ならないからです。 初期化に使う「大きな値」は有効距離より大きければ何でもいいのですが、 ここでは有効距離より1大きい数にしています。
タイル走査

最大有効距離内のタイルすべてが収まる最小の矩形内のタイルを走査します。
各タイルに対する処理は別のコモンイベントに任せます。
タイル毎の処理

タイルごとにアイテムが存在するかどうかとその距離を調べます。
これまでに発見したアイテムと距離が同じかそれより遠い場合には調べる意味がないので、 最初にそれをチェックしています。
今回の実装の最がっかりポイントなのですが、 「アイテムが存在するかどうか」を「イベントが存在するかどうか」で判定しています。 つまり、すべてのイベントに対してダウジングが反応します(!?)。 全然実用的じゃないですね。 まあ、そもそもコモンイベントによる実装自体が実用的じゃないんですが……。
コモンイベントから取得できるタイルの情報はいくつかありますが、 発見後に消滅させられるものと考えるとイベントくらいしか思いつきませんでした。 ちなみに、イベントの消滅も「イベントの一時消去」では効かないので、 マップの遥か彼方へとイベントを吹っ飛ばして消し去っています。
この記事執筆中に思いついた別案として、 「奇数のリージョンID上にあるイベント」 というように条件を絞り込めばもう少し使えそうかなとは思いますが、 どうせ実際のプロダクトには使わないのでこのままにしておきます。
距離の計算

プレイヤーと現在タイルとのマンハッタン距離を計算します。
絶対値の和をとるだけなのですが、まず絶対値をとるのが面倒という……。
目標位置の計算

タイル走査の結果を元に、指示点の目標位置を計算します。
発見できなかった場合と、プレイヤーの真下にアイテムがあった場合には目標位置は中心です。 それ以外の場合にはアイテムのある方向の円周上になります。
目標位置(反応時)

アイテムのある方向の円周上の点の座標を計算します。
atan2で角度を取得してから、cosとsinでそれぞれX座標とY座標を算出します。
この際、あらかじめ数値の倍率に半径を掛けておくことで、cosとsinの結果が半径倍されます。
目標位置(非反応時)
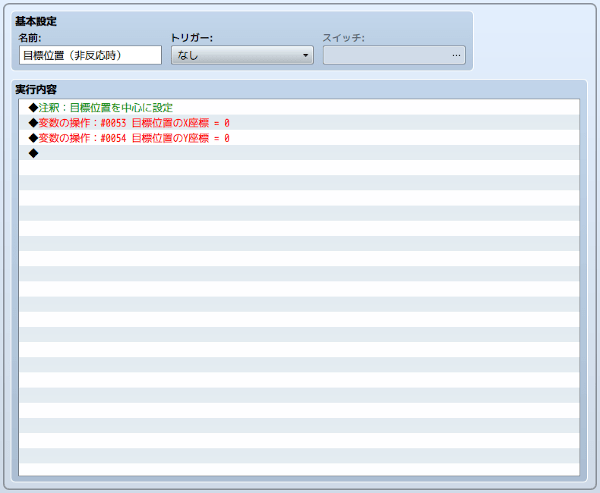
指示点の目標位置を中心に設定します。
現在位置の更新

目標位置に向かうように指示点の現在位置を更新します。
処理の大部分は移動速度が設定された最大値を超えていないかのチェックです。 目標位置に一瞬で移動した場合の移動距離(ユークリッド距離)を、 三平方の定理(ピタゴラスの定理)で算出したいのですが、平方根を計算する術がありません。 そこで発想を変えて、最大値の方を二乗することで二乗した値同士の比較でチェックします。 正の数の大小関係は値を二乗しても変わらないため、これで問題ありません。
移動量の修正

最大移動速度を超えてしまう場合に移動量を調整します。
atan2で移動方向を取得してから、
cosとsinで最大移動速度に一致するようにX方向とY方向の移動量を算出します。
揺れの更新

X方向、Y方向それぞれの揺れの変位を計算します。
ここではX方向とY方向の設定値を変数に入れるだけで、 実際の計算は別のコモンイベントで行います。
揺れの周期の決定

揺れの最小周期と最大周期の間をアイテムとの距離に合わせて補間します。
補間の方法は線形補間と呼ばれるもので、
tを0から1の範囲の値としてa(1 - t) + btという式でaとbの間の値を得ます。
tが0ならaに一致して、1ならbに一致します。
しかし、小数を扱うのは面倒なので、
ここでは適当な重みuとvを使って(au + bv) / (u + v)という式に変形して使っています。
t = v / (u + v)とすれば一致するのがわかると思います。
あとはこの重みを距離に応じて設定するだけです。 aを最小周期、bを最大周期とすると、 vをアイテムまでの距離、u+vを最大有効距離とすればOKです。
揺れの変位の計算

揺れの設定値に従って、揺れの位相を更新し、揺れによる変位を求めます。
揺れはA sin(θ + 2π/T)という式で計算しています。
Aが振幅、Tが周期で、θが前フレームの位相です。
コモンイベントの前半部分では、 周期から角速度を計算して、それに従って位相をずらしています。 設定値との兼ね合いや扱いやすさから、この時点では度数法を使っています。
後半部分では現フレームの位相の範囲を[0,360)から[-180,180)に調整し、
弧度法へと変換した後に振幅倍したsin関数を適用しています。
表示の更新

現フレームの表示位置を計算した後に、ダウジング表示のピクチャを移動させます。
表示位置の計算

現フレームの表示位置を計算します。
いくつかの座標は計算の精度を上げるためにn倍されているため、nで割って元の倍率に戻します。
atan2(y,x)

atan2の計算その1です。
すべての計算が第一象限で行われるように入力と出力を変換して、あとはatan2(y,x)'に任せます。
atan2(y,x)'

atan2の計算その2です。
y/xの値が1以下になるように入力と出力を変換して、arctan(y/x)の近似計算を呼び出します。
arctan(x) [0,1]
![f:id:fspace:20190809195855p:plain コモンイベント『arctan(x) [0,1]』](https://cdn-ak.f.st-hatena.com/images/fotolife/f/fspace/20190809/20190809195855.png)
arctanの計算です。
入力の倍率(S_x)と出力の倍率(S_theta)に注意して、
マクローリン展開による近似式x - x^3 / 3を計算します。
sin(theta)

sinの計算その1です。
角度が0からπ/2の間になるように入力と出力を変換して、あとはsin(theta)'に任せます。
sin(theta)'

sinの計算その2です。
角度が0からπ/4の間になるように入力と出力を変換して、sinの近似計算を呼び出します。
sin(theta) [0,PI/4]
![f:id:fspace:20190809195907p:plain コモンイベント『sin(theta) [0,PI/4]』](https://cdn-ak.f.st-hatena.com/images/fotolife/f/fspace/20190809/20190809195907.png)
sinの計算その3です。
入力の倍率(S_theta)と出力の倍率(S_x)に注意して、
マクローリン展開による近似式x - x^3 / 6を計算します。
cos(theta)

cosの計算その1です。
角度が0からπ/2の間になるように入力と出力を変換して、あとはcos(theta)'に任せます。
cos(theta)'

cosの計算その2です。
角度が0からπ/4の間になるように入力と出力を変換して、cosの近似計算を呼び出します。
cos(theta) [0,PI/4]
![f:id:fspace:20190809195919p:plain コモンイベント『cos(theta) [0,PI/4]』](https://cdn-ak.f.st-hatena.com/images/fotolife/f/fspace/20190809/20190809195919.png)
cosの計算その3です。
入力の倍率(S_theta)と出力の倍率(S_x)に注意して、
マクローリン展開による近似式1 - x^2 / 2を計算します。
PI

πの取得です。
指定倍率(S_theta)の円周率を取得します。
おわりに
めちゃくちゃ長いですね……全部まともに読んだ人がいたならお疲れさまでした。
元々プラグインをつくれない人たちに向けたパフォーマンスだったはずなんですが、 途中からもはや誰向けなのかよくわからなくなってますね……。 ただまぁ、プログラミングというのがそれなりに手間と技術が必要な作業だと感じてもらえればいいなと思います。 ココナラのリクエストボードなんかみてると、 プログラムに対する一般の人の料金感覚と実際の相場が10倍から100倍くらい違うみたいなので……。
最後に自分でネタ振っといて投げっぱなしなのもなんなので、一言。
『コモンイベントの ちからって すげー!』
執筆時のRPGツクールMVのバージョン:1.6.2