【Unity】 Quaternion API解説 - エフアンダーバー

Quaternion（クォータニオン、四元数）は回転操作において重要な数です。しかし、回転という操作がなかなか想像しづらいことや、Quaternionの扱いに少し癖があることなどから、結構ハマりやすいところだと思います（というか、自分がよくハマります）。そこで、UnityにおけるQuaternionのAPIとその注意点についてまとめてみました。

この記事ではQuaternionの理論についてはほとんど触れません。 Quaternionの理論について知りたい場合には過去記事や他所の記事を参照してください。

www.f-sp.com

基本的な使い方についてはこちら。

www.f-sp.com

Quaternion API
解説
参考
ユニティちゃんライセンス
おわりに

Quaternion API

とりあえずAPIの一覧。

重要度は主観です。必要性というよりは有用性や利用頻度を重視しててきとーに決めました。

名前	説明	重要度
`identity`	恒等回転（読み込み専用）。	★★★★★
`eulerAngles`	回転をオイラー角として取得。	★★☆☆☆
`this[int]`	インデクサ。	★☆☆☆☆
`w`	Quaternionのw要素。	★☆☆☆☆
`x`	Quaternionのx要素。	★☆☆☆☆
`y`	Quaternionのy要素。	★☆☆☆☆
`z`	Quaternionのz要素。	★☆☆☆☆
`Quaternion`	コンストラクタ。	★☆☆☆☆
`Set`	w,x,y,z要素に値を設定。	★☆☆☆☆
`SetFromToRotation`	ある方向からある方向への回転に設定。	★☆☆☆☆
`SetLookRotation`	指定した向きを向くための回転に設定。	★☆☆☆☆
`ToAngleAxis`	回転の角度と回転軸を取得。	★★☆☆☆
`Angle`	二つのQuaternionの間の角度を取得。	★★★☆☆
`AngleAxis`	角度と回転軸を指定して回転を作成。	★★★★★
`Dot`	Quaternionの内積を計算。	★★☆☆☆
`Euler`	オイラー角表現から回転を作成。	★★★★☆
`FromToRotation`	ある方向からある方向への回転を作成。	★★★★☆
`Inverse`	逆Quaternionを作成。	★★★★★
`Lerp`	線形補間。	★★★☆☆
`LerpUnclamped`	[0,1]に定義域を制限しない線形補間。	★★☆☆☆
`LookRotation`	指定した向きを向くための回転を作成。	★★★★☆
`RotateTowards`	最大回転量を制限した補間。	★★★☆☆
`Slerp`	球面線形補間。	★★★★☆
`SlerpUnclamped`	[0,1]に定義域を制限しない球面線形補間。	★★☆☆☆
`*`演算子	回転の合成。	★★★★★
`*`演算子	回転の適用。	★★★★★
`==`演算子	等値判定。	★★★☆☆

解説

重要度 ★★★★★

`identity`

identityは恒等回転（無回転）を表すQuaternionを取得するプロパティです。

移動操作における零ベクトルのようなもので、初期状態の回転値を表すためによく使います。

「無回転」とはいっても、その値は0ではないためdefault(Quaternion)とは値が違います。 C#による初期化処理に任せると無効な回転になってしまうため、 Quaternionを初期化する必要がある場合にはしっかりとQuaternion.identityを代入します。

// 複数の回転の合成をきれいに書きたいときにも便利
Quaternion rot = Quaternion.identity;
rot = Quaternion.AngleAxis(15.0f, Vector3.right) * rot;
rot = Quaternion.AngleAxis(45.0f, Vector3.up) * rot;
...

`AngleAxis`

AngleAxisは回転角度と回転軸からQuaternionを作成する関数です。

これはQuaternionを作成する最も基本的な方法です。どの向きを軸としてどれくらいの角度回転させるかを指定します。

Unityは左手座標系のため、回転方向は軸の正方向を向いて反時計回りです。左手の親指だけを立てて軸の方を向けたときに、親指に対してそれ以外の指が向いている方向です（左ねじ）。ちなみに左手座標系は、左手をピストルの形にしてさらに中指を垂直に立てたとき、親指をX軸、人差し指をY軸の正方向に向けると、中指がZ軸の正方向を向くような座標系を言います（右手でやると逆向きになります）。

QuaternionのAPI全体に言えることですが、角度の指定が弧度法（ラジアン）ではなく度数法（度）なことに注意が必要です。特にベクトルの内積や外積の結果から逆三角関数を用いて得た角度などを利用する場合には、 Mathf.Rad2Degを乗算して度数法に直すことを忘れないようにしてください。

また、Quaternionによる回転は原点中心の回転です。他の点を中心として回転させたい場合には、その点が原点になるように平行移動した後に回転を適用し、再度同じ量だけ逆向きに平行移動します。

// 点(1,2,3)を(1,1,1)を中心としてY軸周りに180度回転
Vector3 p = new Vector3(1f, 2f, 3f);
p -= Vector3.one;
p = Quaternion.AngleAxis(Mathf.PI * Mathf.Rad2Deg, Vector3.up) * p;
p += Vector3.one;
Debug.Log(p); // (1.0, 2.0, -1.0)

`Inverse`

Inverseは逆Quaternionを作成する関数です。

逆Quaternionは逆行列のようなもので、元のQuaternionの回転を打ち消すような回転、つまりは同じ軸で逆向きの回転を表します。そのため、元のQuaternionと逆Quaternionを合成すると、回転を打ち消し合ってQuaternion.identityの値と一致します（ただし、計算誤差があるため完全に一致するとは限らない）。

// 逆Quaternionと元のQuaternionを合成
Quaternion rot = Quaternion.AngleAxis(60.0f, Vector3.forward);
Quaternion q1 = rot * Quaternion.Inverse(rot);
Quaternion q2 = Quaternion.Inverse(rot) * rot;

Debug.Log(Quaternion.identity); // (0.0, 0.0, 0.0, 1.0)
Debug.Log(q1);                  // (0.0, 0.0, 0.0, 1.0)
Debug.Log(q2);                  // (0.0, 0.0, 0.0, 1.0)

`*`演算子（`Quaternion`と`Quaternion`）

Quaternion同士の間に定義される*演算子はQuaternionの乗算を表します。

Quaternionは乗算によって合成することができます。すなわち、乗算によって2つのQuaternionによる二段階の回転を、同一の結果を生む1つのQuaternionによる一段階の回転にすることができます。複雑な組み合わせによる回転も、あらかじめ回転同士を合成しておけば、適用の処理が一回で済むので高速化が可能です。

Quaternionの乗算は行列と同じで、左右どちらから掛けるかによって計算結果が異なります（交換法則が成り立たない）。つまり、二つの回転のどちらを先に適用するかという問題があるわけです。 Unityでは、右側に掛けたものから順に回転が適用されるというルールがあるため、先に適用したい回転を右側に書きます。

C#には*=演算子という乗算と代入を同時に行う演算子がありますが、言語仕様上この演算子の左辺値は乗算時にも左辺値となるため、この演算子を用いると後から掛けたものほど先に適用されるというわかりづらい記述になります。そのため、Quaternionに対しては*=演算子を使わないことをおすすめします。

注意点として、先に適用する回転によって、後に適用される回転の軸が回転することはありません。回転の順番を考える時にはこのことを念頭に置いておくといいと思います。

// 乗算の順序で結果が変化
Quaternion rot1 = Quaternion.AngleAxis(90.0f, Vector3.forward);
Quaternion rot2 = Quaternion.AngleAxis(90.0f, Vector3.up);

Debug.Log(rot2 * rot1 * Vector3.one); // (1.0, 1.0, 1.0)
Debug.Log(rot1 * rot2 * Vector3.one); // (-1.0, 1.0, -1.0)

`*`演算子（`Quaternion`と`Vector3`）

QuaternionとVector3の間に定義される*演算子は座標に対して回転を適用します。

ベクトルに対して*演算子を適用する場合には、Quaternionを必ず左側に書く必要があります *1。 Unityで右側から掛けたものから順に回転が適用されるのはこの仕様のためです（ベクトルの近くに掛けられたものほど先に適用される）。

余談ですが、この操作は*演算子で表されますが、数学的な意味では乗算ではありません。そのため、Unity以外では*演算子ではなく関数で表されることもあります。

// 点(1,1,1)をY軸周りに30度回転
Quaternion rot = Quaternion.AngleAxis(30.0f, Vector3.up);
Vector3 p = Vector3.one;

Debug.Log(rot * p); // (1.4, 1.0, 0.4)

// 逆には書けない
// Debug.Log(p * rot);

// 実際にはこんな感じの計算
Quaternion q = rot * new Quaternion(p.x, p.y, p.z, 0f) * Quaternion.Inverse(rot);
Debug.Log(new Vector3(q.x, q.y, q.z)); // (1.4, 1.0, 0.4)

重要度 ★★★★☆

`Euler`

Eulerはオイラー角表現からQuaternionを作成する関数です。

オイラー角は各座標軸周りの回転角度による回転の表現方法です *2。エディタ上でTransformコンポーネントのRotationの表示に利用されている形式です。キャラクター等の前後左右がはっきりとしたモデルを回転させる際には、任意軸回転よりもオイラー角の方が直感的なためよく使われます。

オイラー角では各座標軸周りで計三回の回転を行うため、回転の順番が重要になります。 UnityではZ軸、X軸、Y軸の順番を採用しています。 Unityは正面をZ軸正方向、頭上をY軸正方向と定めているため、この回転順が最も直感的になります。

例えば戦闘機による3DSTGを仮定すると、上下と左右それぞれに機首を向ける回転とアクロバット飛行的なローリングの三軸回転を考えるのがわかりやすいと思います。このとき戦闘機が初期状態においてY軸正方向を上側にZ軸正方向を向いているとすると、ローリング（Z軸）、上下方向（X軸）、左右方向（Y軸）の順番でないと想定通り回転しません *3。

オイラー角を使う上での注意点としてジンバルロックの問題があります。ジンバルロックは三軸回転において、二番目の回転軸（UnityではX軸）が90度回転したときに他の二つの回転方向が一致してしまう現象です。回転軸が二つしかないのと同じ状態なので回転の自由度が減少します。もともとジンバルという姿勢制御装置の部品で起こる現象で、ある向きに対して回転できなくなってしまう（ロックされている）状態を指します。とはいえこれは物理的にうまく回転しないという話であって、コンピュータ上では別の回転値を与えれば当然回転します。

では何が問題かというと、回転軸が重なることで同じ姿勢を表す回転値が無数に存在してしまうことです。これにより、オイラー角表現における値が大きく異なるにもかかわらず、姿勢が非常に近い回転が存在してしまいます。このような二つの回転をオイラー角表現のまま補間してしまうと、姿勢が近いにも関わらず大きく変化しながら補間してしまいます。

Quaternionは任意の姿勢をほぼ一意に表せる（過去記事参照）ため、オイラー角であってもQuaternionに変換してから補間する場合にはジンバルロックの問題は発生しません。ただし、オイラー角による補間とQuaternionによる補間の結果は一致しないため、アニメーションに多少の変化が出る可能性があります。

// Quaternionとオイラー角の比較
Vector3 e1 = new Vector3(-90.0f, 200.0f, -200.0f);
Vector3 e2 = new Vector3(-90.0f, 0.0f, 0.0f);
Vector3 e3 = new Vector3(-80.0f, 0.0f, 0.0f);
Quaternion q1 = Quaternion.Euler(e1);
Quaternion q2 = Quaternion.Euler(e2);
Quaternion q3 = Quaternion.Euler(e3);
Quaternion rotA = Quaternion.Slerp(q1, q3, 0.5f);
Quaternion rotB = Quaternion.Euler(Vector3.Lerp(e1, e3, 0.5f));

Debug.Log(e1 == e2); // False
Debug.Log(q1 == q2); // True
Debug.Log(q1 * Vector3.forward);   // (0.0, 1.0, 0.0)
Debug.Log(q3 * Vector3.forward);   // (0.0, 1.0, 0.2)
Debug.Log(rotA * Vector3.forward); // (0.0, 1.0, 0.1)
Debug.Log(rotB * Vector3.forward); // (0.1, 1.0, 0.0)

`LookRotation`

LookRotationは指定した向きを向くためのQuaternionを作成する関数です。

LookRotationにはforwardとupwardsという二つの向きを指定します。 forwardは正面方向を、upwardsは上方向を表し、結果のQuaternionを適用するとZ軸の正方向がforwardの向きに、Y軸の正方向がupwards寄りの向きになるように回転します。なぜ『寄り』なのかというと、Z軸とY軸が直交していなければならない一方で、forwardとupwardsが直交しているとは限らないからです *4。

LookRotationではまずforwardの向きをZ軸正方向と決めます。その後、upwardsとforwardの外積の向き（二軸に直交する向き）をX軸正方向とします。最期にZ軸とX軸に直交する向きをY軸として（左手座標系となるように正方向を決める）、その座標系への回転を表すQuaternionを返します。 forwardとupwardsが平行だった場合には、外積が零ベクトルになるためエラーとなります。 upwardsは省略が可能で、その場合にはY軸正方向(0,1,0)が使われます。

LookRotationは対象が回転適用前にY軸正方向を上にしてZ軸正方向を向いているという仮定のもとでうまく動作する関数です。使用の際には前提を満たしているかどうか確認する必要があります。

// 上下逆さまでX軸正方向を向く
Vector3 forward = Vector3.right;
Vector3 upwards = Vector3.down;
Quaternion rot = Quaternion.LookRotation(forward, upwards);

Debug.Log(rot * Vector3.forward); // (1.0, 0.0, 0.0)
Debug.Log(rot * Vector3.up);      // (0.0, -1.0, 0.0)

// 回転後の各座標軸
Vector3 z = forward;
Vector3 x = Vector3.Cross(upwards, z).normalized;
Vector3 y = Vector3.Cross(z, x);

Debug.Log(x == rot * Vector3.right);   // True
Debug.Log(y == rot * Vector3.up);      // True
Debug.Log(z == rot * Vector3.forward); // True

`FromToRotation`

FromToRotationはある方向からある方向へと回転させるQuaternionを作成する関数です。

FromToRotationでは開始方向と終了方向を指定することで、開始方向を終了方向へと向ける回転を表すQuaternionを返します。ここで問題となるのが、開始方向を終了方向へと向ける回転というのは無数に存在するということです。この関数で取得できるのはそのうち最も回転角度の小さいものになります。

使い方が簡単なので、使い勝手がよさそうに見えますが過信するとバグに陥りやすい関数です。例えば、キャラクターにある方向を向かせたいからといって使ってしまうと、キャラクターが斜めに傾いたりします。 LookRotationを見ればわかる通り、モデルの向きというのは正面方向だけでは決まらないのです。

f:id:fspace:20170811193320g:plain — 同じ開始方向と終了方向の回転は無数に存在

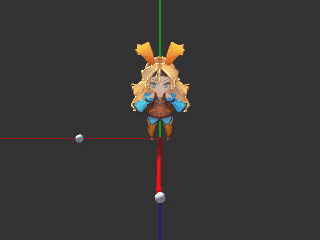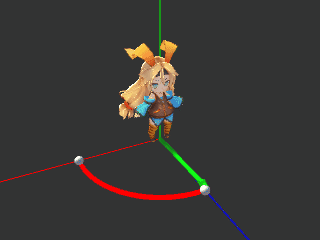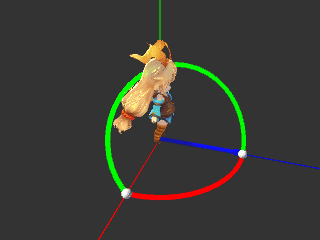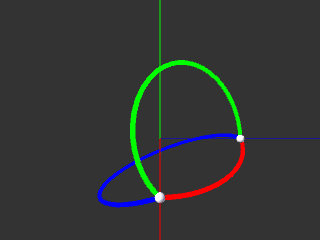
// (1,1,1)の方向を向く回転
Quaternion rot1 = Quaternion.FromToRotation(Vector3.forward, Vector3.one);
Quaternion rot2 = Quaternion.LookRotation(Vector3.one);

// 正面方向は同じ
Debug.Log(rot1 * Vector3.forward); // (0.6, 0.6, 0.6)
Debug.Log(rot2 * Vector3.forward); // (0.6, 0.6, 0.6)

// それ以外は異なる
Debug.Log(rot1 * Vector3.right);   // (0.8, -0.2, -0.6)
Debug.Log(rot2 * Vector3.right);   // (0.7, 0.0, -0.7)
Debug.Log(rot1 * Vector3.up);      // (-0.2, 0.8, -0.6)
Debug.Log(rot2 * Vector3.up);      // (-0.4, 0.8, -0.4)

`Slerp`

Slerpは二つのQuaternionの間を球面線形補間(Spherical Linear intERPolation)する関数です。

球面線形補間は二つのQuaternionとその影響度の割合から中間的な回転を表すQuaternionを作成します。「球面」という言葉がついているので何か特殊な補間のように思えるかもしれませんが、Quaternionの回転としてはこれが最も基本的な補間です。回転を表すQuaternionは球面上にあるためそれらを線形補間しようとすると球面線形補間となるのです（詳細は過去記事参照）。

影響度の割合は[0,1]の範囲の値を与えることで指定します。 0は先に指定したQuaternionの影響度100%、1は後に指定したQuaternionの影響度100%です。中間値を与えるとそれらの影響度が線形に（比例するように）変化していきます。また0より小さい値を与えた場合には0、1より大きい値を与えた場合には1として扱われます(clamp)。

// 角度について線形に補間される
Quaternion a = Quaternion.AngleAxis(-90.0f, Vector3.up);
Quaternion b = Quaternion.AngleAxis(90.0f, Vector3.up);
Quaternion c = Quaternion.AngleAxis(45.0f, Vector3.up);
Quaternion q1 = Quaternion.Slerp(a, b, 0.75f);
Quaternion q2 = Quaternion.Slerp(b, a, 0.25f);
Quaternion q3 = Quaternion.Slerp(a, b, 2.0f);

Debug.Log(q1 == c); // True
Debug.Log(q2 == c); // True
Debug.Log(q3 == b); // True

重要度 ★★★☆☆

`Angle`

Angleは二つのQuaternionの間の角度を取得する関数です。

二つのQuaternionの角度と言われてもいまいちピンとこないかもしれませんが、二つの回転がどれくらい似ているかの尺度だと考えると使い道が想像しやすいかもしれません。角度が小さいほど似ている回転になります。回転合成の繰り返しによって特定の回転にぴったり一致するということはほぼあり得ないため、ある向きに一致するという判定をしたいときには、等値比較よりも、角度が閾値以下であるかどうかを判定した方がいい場合があります。

一般に二つのQuaternionのなす角度というと、正規化したQuaternionの内積の結果に逆余弦関数を適用した値を指しますが、この関数はその2倍の値を返します。 3次元空間の回転に用いるQuaternionは指定した回転角度の半分の値を用いるため（過去記事参照）、 2倍して指定した回転角度と同じになるようにしているものと思われます。つまり、正確にはQuaternion間の角度ではなく、片方の姿勢からもう片方の姿勢へと回転させる際の回転角度の絶対値を表します。

この関数によって取得した角度は弧度法ではなく度数法なので、三角関数の引数などに用いる場合にはMathf.Deg2Radを掛ける必要があります。

// 片方の姿勢からもう片方の姿勢へと回転させる際の回転角度と一致
Quaternion q1 = Quaternion.AngleAxis(90.0f, Vector3.right);
Quaternion q2 = Quaternion.AngleAxis(90.0f, Vector3.forward);
Quaternion delta = q2 * Quaternion.Inverse(q1);

float angle;
Vector3 axis;
delta.ToAngleAxis(out angle, out axis);

Debug.Log(Quaternion.Angle(q1, q2)); // 120
Debug.Log(angle);                    // 120

`Lerp`

Lerpは二つのQuaternionの間を線形補間(Linear intERPolation)する関数です。

Quaternionの補間は基本的に球面線形補間(Slerp)を使います。しかし、球面線形補間は三角関数を何度か適用するため、膨大な回数繰り返す場合には少しだけ処理が重いです。そこで、精度を犠牲にして高速化するための手段として線形補間と正規化による方法を使うことできます。

線形補間はQuaternion間の角度が0に近づくほど球面線形補間の結果に近づきます（過去記事参照）。そのため角度が小さい場合にはそれほど違和感なく補間できますが、角度が大きい場合には指定した影響度がうまく反映されずおかしな補間となります。

ちなみに、球面線形補間より速いといっても時間としては本当に微小なものです。そもそも球面線形補間は体感できるほど遅い処理でもありませんので、本当に膨大な回数実行する可能性がある場合にのみ使用することをおすすめします。

// 補間の角度が大きいと誤差も大きく
Quaternion a = Quaternion.AngleAxis(-90.0f, Vector3.up);
Quaternion b = Quaternion.AngleAxis(90.0f, Vector3.up);
Quaternion c = Quaternion.AngleAxis(45.0f, Vector3.up);
Quaternion lerp1 = Quaternion.Lerp(a, b, 0.75f);
Quaternion lerp2 = Quaternion.Lerp(b, c, 0.75f);
Quaternion slerp1 = Quaternion.Slerp(a, b, 0.75f);
Quaternion slerp2 = Quaternion.Slerp(b, c, 0.75f);

Debug.Log(lerp1 == c);  // False
Debug.Log(slerp1 == c); // True
Debug.Log(Quaternion.Angle(lerp1, slerp1)); // 8.130105
Debug.Log(Quaternion.Angle(lerp2, slerp2)); // 0.1119058

`RotateTowards`

RotateTowardsは二つのQuaternionの間を最大回転量を指定して補間する関数です。

Slerpでは補間に影響度を指定しましたが、この関数では最大回転量を指定します。 Slerpが中間的な回転を得る汎用性の高い関数である一方で、この関数は急激な変化を防ぐことに特化した関数です。一度の変化に許容できる最大の回転量を指定することで急速な回転による不自然さを緩和させるために使います。とはいえ、最大回転量のみによる制御というのはかなり簡易的なものなので、挙動にこだわるのであれば角速度やアニメーションを導入した方がよいと思います。

最大回転量に正の値を指定すると近い方向から、負の値を指定すると遠い方向から回転します。ただし不思議なことに、正の値では目標回転値で止まるのに対し、負の値では目標回転値に達してもなお回転を続けます。直感的でないので負の値は指定しないことをおすすめします。

// 最大回転量で制限
Quaternion a = Quaternion.AngleAxis(-90.0f, Vector3.up);
Quaternion b = Quaternion.AngleAxis(90.0f, Vector3.up);
Quaternion c = Quaternion.AngleAxis(45.0f, Vector3.up);
Quaternion q1 = Quaternion.RotateTowards(a, b, 135.0f);
Quaternion q2 = Quaternion.RotateTowards(a, b, 720.0f);
Quaternion q3 = Quaternion.RotateTowards(a, b, -720.0f);

Debug.Log(q1 == c); // True
Debug.Log(q2 == b); // True
Debug.Log(q3 == a); // True

`==`演算子, `!=`演算子

==演算子は二つのQuaternionが一致するかどうかを判定します。 !=演算子は二つのQuaternionが一致しないかどうかを判定します。

==演算子と!=演算子は他のUnity構造体（ベクトル等）と同様、完全には一致していなくても近い値であれば一致と判定してくれます。そのため計算誤差があっても等値判定が可能です。

Quaternionにはその仕組み上、同じ回転を表す異なるQuaternionが二つずつ存在します（過去記事参照）。しかし、==演算子や!=演算子はこれらを同じQuaternionとはみなさないため注意が必要です。これらを同じとみなしたい場合にはDotを利用します。

// 同じ回転を表すQuaternionの等値判定
Quaternion q1 = Quaternion.AngleAxis(90.0f, Vector3.up);
Quaternion q2 = Quaternion.AngleAxis(90.0f + 360.0f, Vector3.up);
Quaternion q3 = Quaternion.AngleAxis(90.0f + 720.0f, Vector3.up);

Debug.Log(q1 == q2); // False
Debug.Log(q1 == q3); // True
Debug.Log(Mathf.Abs(Quaternion.Dot(q1, q2)) > 1.0f - Quaternion.kEpsilon); // True
Debug.Log(Mathf.Abs(Quaternion.Dot(q1, q3)) > 1.0f - Quaternion.kEpsilon); // True

重要度 ★★☆☆☆

`eulerAngles`

eulerAnglesはQuaternionのオイラー角表現を返すプロパティです。

オイラー角は人間にとってはわかりやすい形式ですが、プログラム的には扱いづらい形式です。そのためオイラー角からQuaternionに変換することは多いですが、逆はそれほどありません。このプロパティを使うのは主に回転値を編集するエディタ拡張を書く場合です。

オイラー角とQuaternionは一対一で対応しないことに注意してください。オイラー角をQuaternionに変換し、再度オイラー角に戻したとしても、元のオイラー角の値とは一致しない可能性があります。

// 様々な要因で元とは異なる値が返る
Quaternion q1 = Quaternion.Euler(360.0f, 450.0f, 540.0f); // 360度以上
Quaternion q2 = Quaternion.Euler(-15.0f, -30.0f, -45.0f); // 負値
Quaternion q3 = Quaternion.Euler(120.0f, 240.0f, 360.0f); // Xが(90,270)の範囲
Quaternion q4 = Quaternion.Euler(90.0f, 60.0f, 30.0f);    // Xが90度または-90度

Debug.Log(q1.eulerAngles); // (0.0, 90.0, 180.0)
Debug.Log(q2.eulerAngles); // (345.0, 330.0, 315.0)
Debug.Log(q3.eulerAngles); // (60.0, 60.0, 180.0)
Debug.Log(q4.eulerAngles); // (90.0, 30.0, 0.0)

`ToAngleAxis`

ToAngleAxisはQuaternionの回転角度と回転軸を取得するメソッドです。

rotationプロパティのようにQuaternionが向きを表している場合には、取得できる角度と軸は初期状態(Quaternion.identity)からの変化分であることに注意が必要です。ある向きとの間の角度を取得したい場合にはAngle関数の利用を検討してください。

実はこのメソッドかなり出来が悪く、軸を反転させるにも関わらず角度が[0,360]の範囲で返ってきます。どうもQuaternionがdouble-cover（過去記事参照）であることを考慮し忘れているみたいです。 360度回転のQuaternionに至っては軸の計算で0割りを起こし、InfinityやNaNといった値が返ってきます。

// 回転値によっては期待した結果にならないことも
Quaternion q1 = Quaternion.AngleAxis(90.0f, Vector3.up);
Quaternion q2 = Quaternion.AngleAxis(450.0f, Vector3.up);
Quaternion q3 = Quaternion.AngleAxis(360.0f, Vector3.up);

float angle1, angle2, angle3;
Vector3 axis1, axis2, axis3;
q1.ToAngleAxis(out angle1, out axis1);
q2.ToAngleAxis(out angle2, out axis2);
q3.ToAngleAxis(out angle3, out axis3);

Debug.LogFormat("{0}: {1}", angle1, axis1); // 89.99999: (0.0, 1.0, 0.0)
Debug.LogFormat("{0}: {1}", angle2, axis2); // 270: (0.0, -1.0, 0.0)
Debug.LogFormat("{0}: {1}", angle3, axis3); // 360: (NaN, -Infinity, NaN)

`Dot`

DotはQuaternionの内積を計算する関数です。

Quaternionの理論についての理解が必要なため使う機会はそう多くないですが、内積の計算結果はいろいろと便利です。例えば、角度比較の際にAngle関数の代わりに使って高速化したり、許容的な等値比較をする際にも利用できます。また、独自の補間関数を定義したい場合にも必要になります。

`LerpUnclamped`, `SlerpUnclamped`

LerpUnclampedとSlerpUnclampedはそれぞれ[0,1]に定義域を制限しないLerpとSlerpです。

稀にですが、[0,1]でない範囲まで補間したい場合というのがあります。例えば、ばねのような力によって一度目標値を通り過ぎてから戻るような挙動を実装したいときなどが考えられます。

重要度 ★☆☆☆☆

`this[int]`, `w`, `x`, `y`, `z`

Quaternionを構成する値を直接変更したい場合にはインデクサや各要素名のフィールドが利用できます。

Quaternionの理論を理解した上で、独自の関数などを定義したい場合に使用します。

コンストラクタ

Quaternionには各要素の値を直接指定するコンストラクタが定義されています。

基本的にはQuaternionは各種関数を利用して作成するため、コンストラクタを直接呼び出す必要はありません。

`SetXXX`

Setから始まる各種メソッドは既存のQuaternionの値を新しい値で書き換えます。

Quaternionを新しい値で書き換えたい場合には代入演算子を利用するのが一般的です。 Setから始まるメソッドを使うと、読みづらい上に間違いやすいため封印推奨です。

参考

ユニティちゃんライセンス

この作品はユニティちゃんライセンス条項の元に提供されています

おわりに

もともと初心者向けにQuaternionの記事を書いていたのですが、余計なことを書きすぎたせいでAPIの部分が難しくなったため分離しました。次回こそ初心者向けの記事になる予定。

アニメGIFを作るために今回初めてTimelineを使ってみましたが、なかなか楽しいですねアレ。まあゲーム製作において、使う場面はかなり限られそうですが・・・

執筆時のUnityのバージョン：2017.1.0f3

*1:ベクトルを列ベクトルとして扱うUnityの行列の仕様に合わせたものと思われる

*2:正確には三軸すべてで回さず、同じ軸で二度回してもいいため『各』座標軸ではないですが

*3:想定通りってなんだと言われると難しいのですが・・・

*4:日本語のスクリプトリファレンスをみると直交していると仮定すると書いてありますが嘘です

Quaternion API

解説

重要度 ★★★★★

identity

AngleAxis

Inverse

*演算子（QuaternionとQuaternion）

*演算子（QuaternionとVector3）

重要度 ★★★★☆

Euler

LookRotation

FromToRotation

Slerp